6 Recurrent Neural Networks
These notes are based on Josh Starmer’s video
In order to work with time series data to predict the following point, we need to use a model which account for a varying amount of inputs. For example, in stock market price prediction, we want to inputs with a varying amount of input values available for each.
Just like other neural network architectures, RNNs take an input and feed it through an activation. However, RNNs loop the input multiple times through the activation in order to obtain an output.
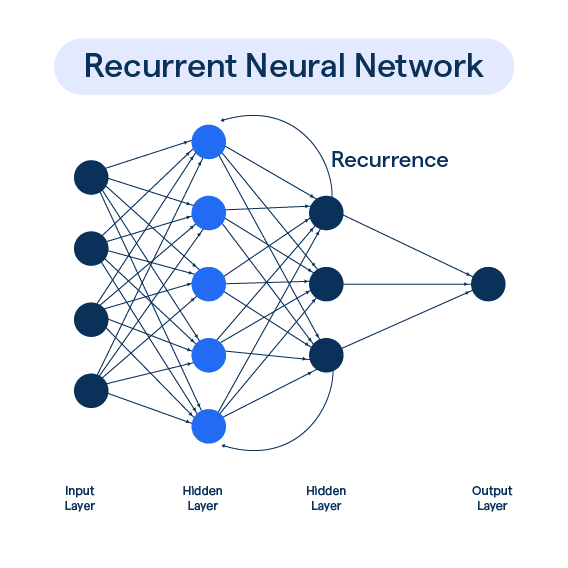
Alternatively, we can think of this process as unrolling the network for sequential time series points.
Suppose:
\begin{align*} & t_{1} \rightarrow ReLU(W_{11}t_{1} + b_{11}) = y_{1} \\ & t_{2} \rightarrow ReLU(W_{12}t_{2} + b_{12} + y_{1}) = y_{2} \\ & \mskip 10mu \vdots \\ & W_{22}y_{2} + b_{2} = \text{ predicted value} \end{align*}
Notice that the output for t_{1} is essentially used as a bias for the second input. This process can be extended to an arbitrary number of sequence numbers. NOTE: even though we unroll the network, the weights and biases are shared!! This means that we never increase the number of weights and biases to train.
6.0.1 Reasons NOT to use RNNs
The more we unroll a network, the harder it becomes to train the network. This leads to the vanishing and exploding gradient problem.
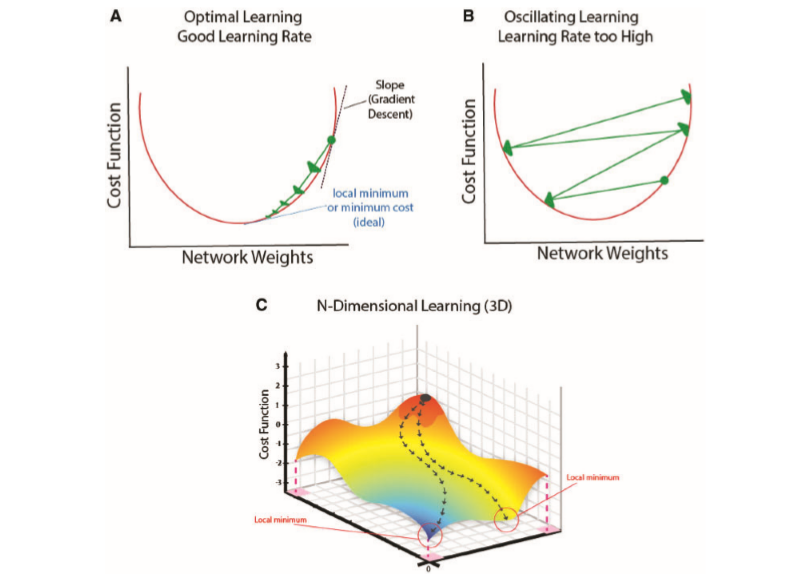
For example, let’s suppose some weight is given for W_{1} (in all unrollings of the network) as 2. Then, every time we run the input, we perform 2 \times y_{i-1} which eventually gets us 2^{n} \times inputs which ends up almost always being a gigantic number, especially for values of n which any reasonable size, say n > 50 or so. This huge number makes it extremely difficult to take small steps towards the correct parameter value. This means that instead of taking small steps, we will end up with extremely large jumps, meaning that we will bounce. However, if you use weight values which are less than 1, then you will obtain values which are extremely small, meaning that the maximum number of training steps will be reached before finding the optimal values.
LSTMs can be used to largely avoid this problem. See Chapter 7