10 Residual connections
This section discusses residual connections based on the information provided by Wong (2021) in his medium article
10.1 Motivation for Residual connections
Deep Neural Networks such as YOLO (see Section 11.2.4.3) allow for greater accuracy and performance. However, deep networks like this make it more difficult for the model to converge during training.
Residual connections help to make training networks easier.
10.2 Formulation
Residual connections - allow data to reach other parts of a sequential network by skipping layers
This flow is depicted well by the following image:
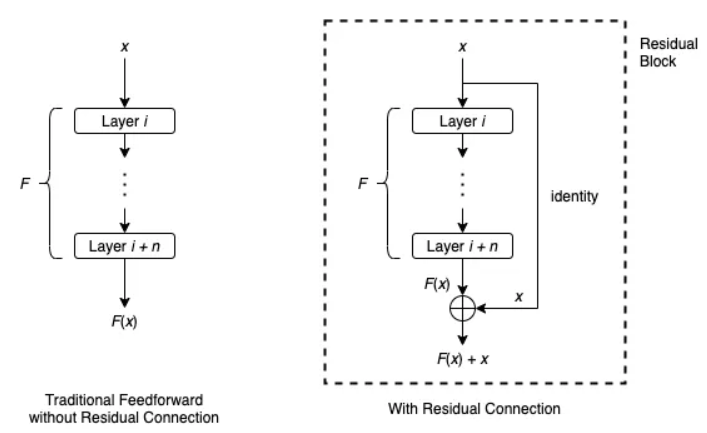
Steps:
- Apply identity mapping to x - perform element-wise addition F(x) + x: this is the residual block
- residual blocks may also include a ReLU actiation applied to F(x) + x. *This works when dimensions of F(x) and x are the same
- If dimensions of F(x) and x are NOT the same, then you can multiply x by some matrix of constants W to scale it. F(x) + Wx
10.3 The Utility of Residual Blocks for Training Deep Networks
Empirical results have demonstrated that residual blocks increase the speed and ease of network convergence. There are a number of suspected reasons as to why this enables such performance gains.